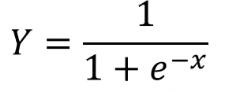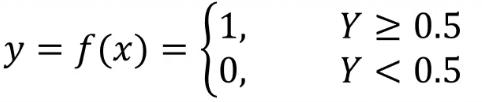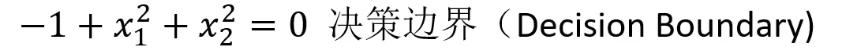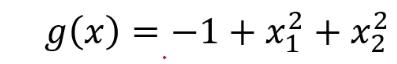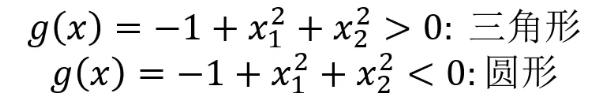机器学习中采用逻辑回归算法解决分类问题

在忙碌的工作中，还是需要抽时间来记录一下学习所得，在上一篇文章中我们谈到了使用线性回归来预测房价的问题，在这篇文章中我们谈一谈逻辑回归。

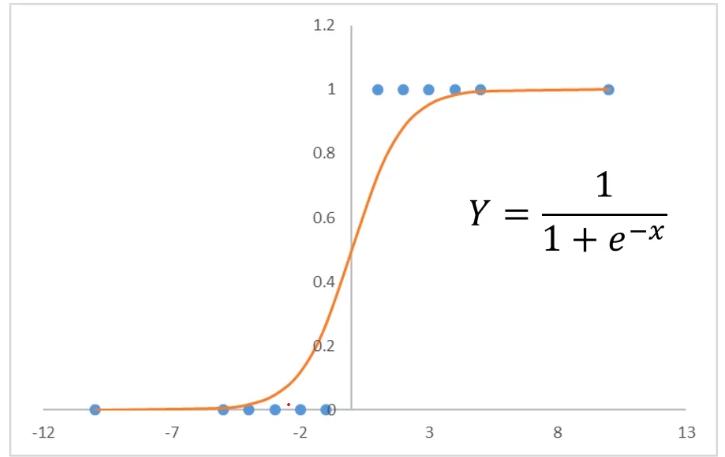
我对逻辑回归的理解

这几天学了一下逻辑回归，总的来说，我认为主要还是用来解决分类问题中的二分类（其实还可以做多分类，但是不是主要），多分类的话可以采用之后所说的非监督学习。在上一篇文章中，我们在线性回归算法中对模型的评估主要是用MSE，R2_score这两种损失函数的方法，而在逻辑回归算法中，我们使用准确率来对模型进行评估。

关于逻辑回归方程

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点：
⭐优点：平滑、易于求导。
⭐缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
Sigmoid函数由下列公式定义：
Sigmoid函数
我们可以再来看一看该方程所对应的图形：
Sigmoid函数图像
可以发现当样本值越大y越接近1，样本值越小y越接近0，以0.5为分界点就可以将y分成以下两种情况。
Sigmoid函数的y
这时负样本就是0，正样本就是1，0和1就是我们给样本定义的标签。在考试通过问题中，可以用1代表通过（pass）,用0代表失败（failed），这样就可以通过标签0和1将失败和通过进行一个分类，就可以很好地解决二分类问题了。

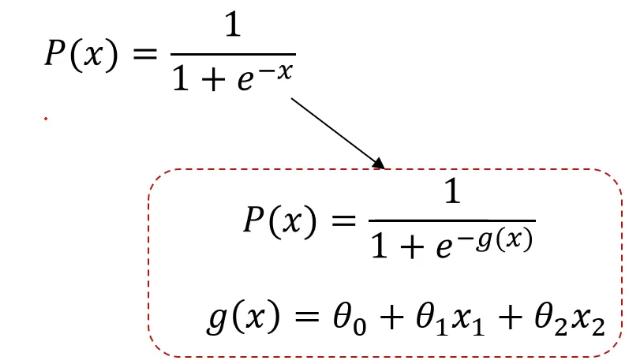
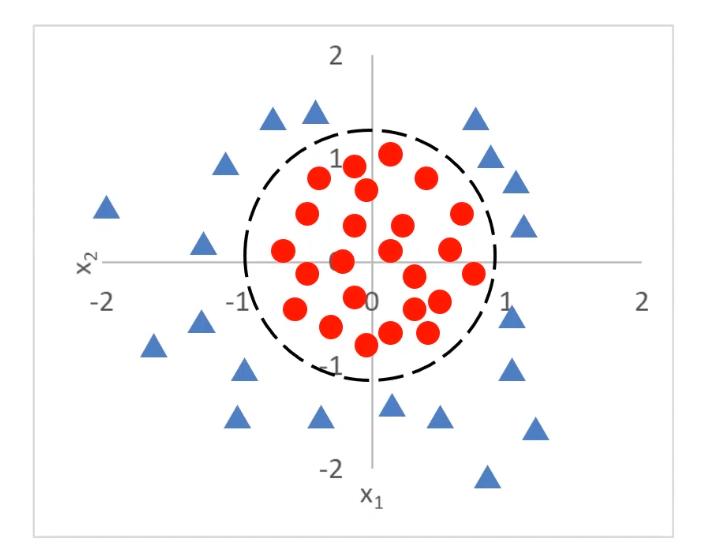
当问题更复杂时，可以用g(x)代替x，然后就可以根据g(x)寻找最合适的决策边界从而解决二分类问题。
Sigmoid函数二分类
比如下面这个图形：
Sigmoid函数二分类图像
此时虚线部分就是它的决策边界
Sigmoid函数二分类图像1
Sigmoid函数二分类图像2
Sigmoid函数二分类图像3

使用逻辑回归算法对考试成绩进行预测

基于examdata.csv数据，建立逻辑回归模型 预测Exam1 = 70, Exam2 = 60时，该同学在Exam3是 passed or failed; 建立二阶边界，提高模型准确度。
⭐实战中我们分别使用一阶边界以及二阶边界，观察两种情况的准确率，发现二阶边界的准确率更高，当然，对于我的理解就是要根据不同的数据采取不同的算法，没有固定那个算法的准确率比较高这样一说。
那么下面我将会贴出代码以及结果。

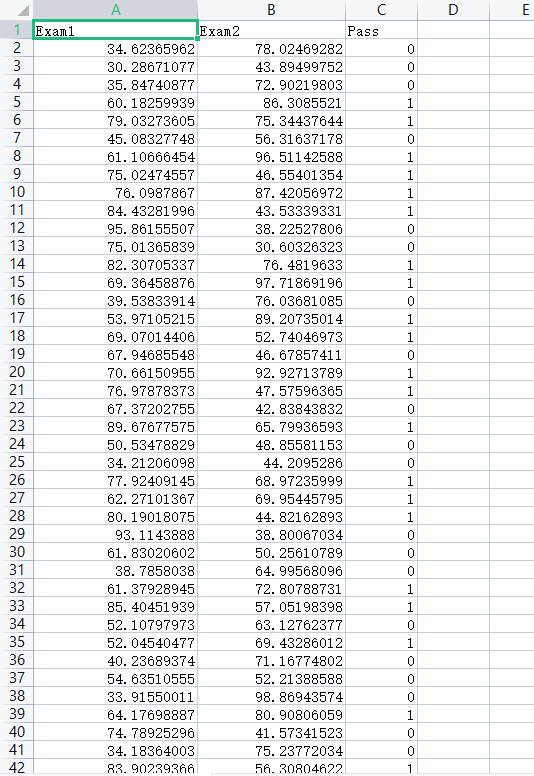
⭐预测数据展示
考试预测数据

⭐代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

data = pd.read_csv('examdata.csv')
#---------------------------------区分通过和未通过
mask = data.loc[:,'Pass']==1

#获取数据
X = data.drop(['Pass'],axis=1)
y = data.loc[:,'Pass']
X1 = data.loc[:,'Exam1']
X2 = data.loc[:,'Exam2']
X1_X1 = X1*X1
X1_X2 = X1*X2
X2_X2 = X2*X2
# 训练R1
LR = LogisticRegression()
LR.fit(X,y)
theta0 = LR.intercept_
theta1 = LR.coef_[0][0]
theta2 = LR.coef_[0][1]
predict_y = LR.predict(X)
result = accuracy_score(y,predict_y)

print(data.head())
fig = plt.figure()
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask])
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.title('Exam1-Exam2')
plt.legend((passed,failed),('passed','failed'))
X2_new = -(theta0+theta1*X1)/theta2
plt.plot(X1,X2_new)
plt.show()
#---------------------------------------------

#训练R2
# X = {'X1':X1,'X2':X2,'X1_X1':X1_X1,'X2_X2':X2_X2,'X1_X2':X1_X2}
# X = pd.DataFrame(X)
# LR2 = LogisticRegression()
# LR2.fit(X,y)
# theta0 = LR2.intercept_
# theta1 = LR2.coef_[0][0]
# theta2 = LR2.coef_[0][1]
# theta3 = LR2.coef_[0][2]
# theta4 = LR2.coef_[0][3]
# theta5 = LR2.coef_[0][4]
# X1_new = X1.sort_values()
# print(theta1,'\n',theta2,'\n',theta3,'\n',theta4,'\n',theta5)
# a = theta4
# b = theta2+theta5*X1_new
# c = theta0+theta1*X1_new+theta3*X1_new*X1_new
# LR2_y = LR2.predict(X)
# result = accuracy_score(y,LR2_y)
# fig2 = plt.figure()
# passed = plt.scatter(data['Exam1'][mask],data['Exam2'][mask])
# failed = plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask])
# X2_new = (-b+np.sqrt(b*b-4*a*c))/(2*a)
#
# plt.plot(X1_new,X2_new)
# plt.xlabel('Exam1')
# plt.ylabel('Exam2')
# plt.title('Exam1-Exam2')
# plt.legend((passed,failed),('passed','failed'))
# plt.show()
# print(result)

⭐一阶边界结果
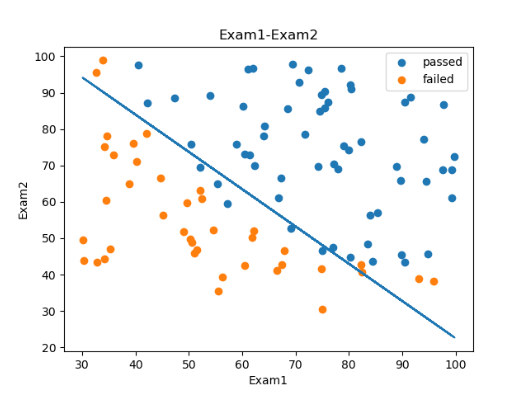
考试预测一阶边界结果

⭐二阶边界结果
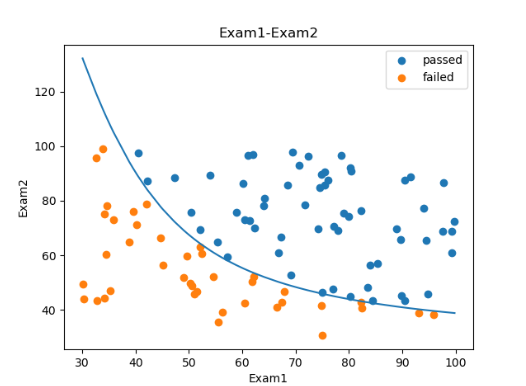
考试预测二阶边界结果

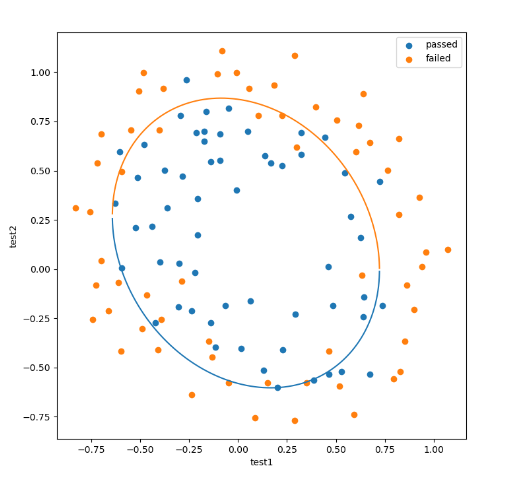
使用逻辑回归算法对芯片进行检测

⭐思路与过程
在这个例子中，思路与上一个例子大同小异，我们首先都是用一阶边界来进行预测，然后发现准确率不高，便采用二阶边界预测，准确率大大提高。将图像可视化，发现两端函数有缺口，原因是画线采用的x区间单位间距较大，我们将其缩小即可。

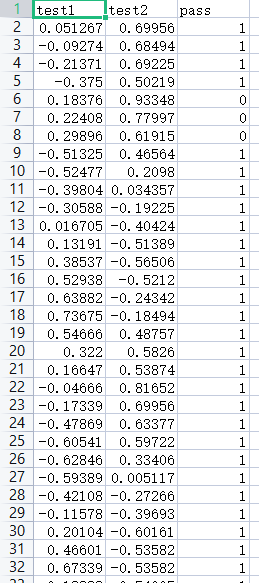
⭐预测数据展示
芯片预测数据

⭐代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
data = pd.read_csv('chip_test.csv')
x = data.drop(['pass'],axis=1)
y = data.loc[:,'pass']
x1 = data.loc[:,'test1']
x2 = data.loc[:,'test2']
mask = data.loc[:,'pass']==1

LR1 = LogisticRegression()
LR1.fit(x,y)
y_predict = LR1.predict(x)
print(accuracy_score(y, y_predict)) # 得出的结果是0.5423728813559322，太低了
# 错误率太高了，我们使用曲线的方式来求解
x1_2 = x1*x1
x2_2 = x2*x2
x1_x2 =x1*x2
x_new = {'x1':x1,'x2':x2,'x1_2':x1_2,'x2_2':x2_2,'x1_x2':x1_x2}
x_new = pd.DataFrame(x_new)
LR2 = LogisticRegression()
LR2.fit(x_new,y)
y_predict = LR2.predict(x_new)
print(accuracy_score(y, y_predict))

x1_new = x1.sort_values()#排序,原因是让后面画图按照次序画图以防止画图很凌乱无序。
theta0 = LR2.intercept_
theta1 = LR2.coef_[0][0]
theta2 = LR2.coef_[0][1]
theta3 = LR2.coef_[0][2]
theta4 = LR2.coef_[0][3]
theta5 = LR2.coef_[0][4]

def f(x1_new):
    a = theta4
    b = theta2+theta5*x1_new
    c = theta0+theta1*x1_new+theta3*x1_new*x1_new
    x2_new_boundary1 = (-b+(np.sqrt(b*b-4*a*c)))/(2*a)
    x2_new_boundary2 = (-b-(np.sqrt(b*b-4*a*c)))/(2*a)
    return x2_new_boundary1,x2_new_boundary2

x1_range = [-0.9 + x/10000 for x in range(0,19000)]
x1_range = np.array(x1_range)
x2_new_boundary1 = []
x2_new_boundary2 = []
for x in x1_range:
    x2_new_boundary1.append(f(x)[0])
    x2_new_boundary2.append(f(x)[1])

#可视化数据
fig1 = plt.figure()
plt.figure(figsize=(8,8))
passed = plt.scatter(x1[mask],x2[mask])
failed = plt.scatter(x1[~mask],x2[~mask])
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.plot(x1_range,x2_new_boundary1)
plt.plot(x1_range,x2_new_boundary2)
plt.show()

⭐二阶边界结果
芯片检测二阶边界结果