机器学习中的线性回归模型预测

⭐什么是机器学习

机器学习是一种实现人工智能的方法，从数据中寻找规律、建立关系,根据建立的关系解决实际问题。

⭐机器学习的分类

监督学习 Supervised Learning

训练数据包括正确的结果

无监督学习 Unsupervised Learning

训练数据不包括正确结果

半监督学习 Semi-supervised Learning

训练数据包括少量正确的结果 (适合样本少)

强化学习 Reinforcement Learning

根据每次结果收获的奖惩进行学习,实现优化

⭐关于损失函数

其中y是真实结果，y’是训练结果。我们要做的事要让y和y’更加接近，也就是说要让J尽可能的小，下面我们贴出公式：
线性回归公式

⭐关于梯度下降法

寻找极小值的一种方法,通过向函数当前点对应梯度(或者近似梯度)的反方向的规定步长距离点进行迭代搜索,直到再极小点收敛。

⭐评估模型表现方法

y与y’的均方误差 MSE 越小越好
R方值接近1最好
画图看图

说了一丢丢理论，我们还是用代码来说明一下比较直观，接下来用一个房价预测的例子来说明一下线性回归模型。首先我们使用的语言是Python，需要的库有： 1. pandas 2. numpy 3. matplotlib 4. sklearn（线性回归使用的库） ⭐注：上面说的库在anaconda都有

接下来我们还需要准备数据集，这边采用的是数据集为usa_housing_price.csv，下图展示的是部分数据：
房屋预测数据

代码展示

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score

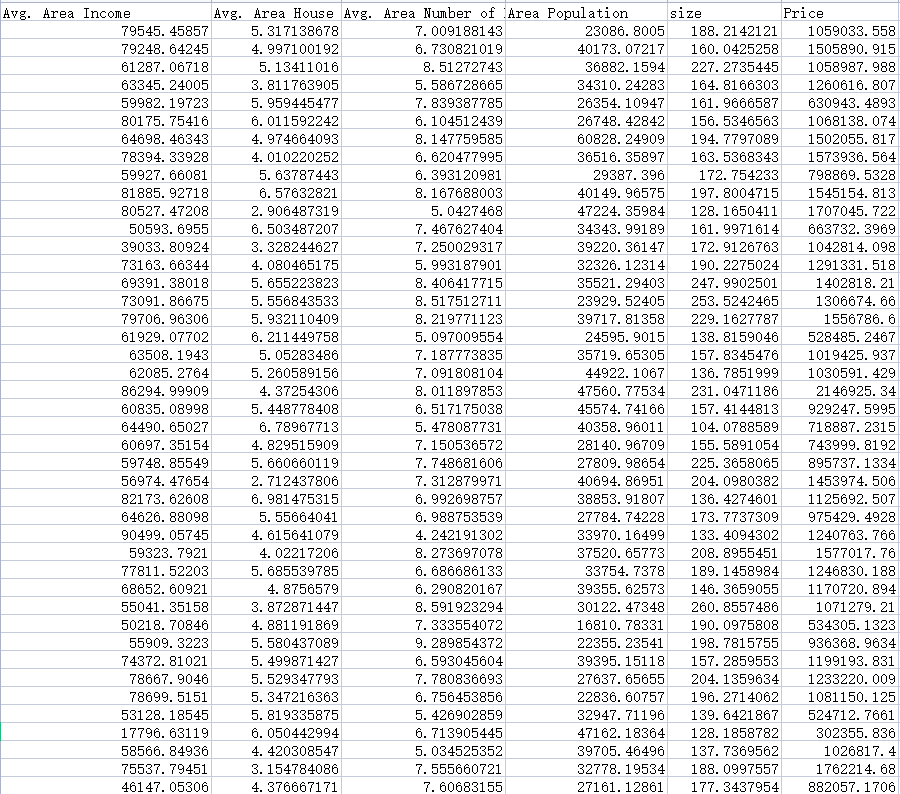
data = pd.read_csv('usa_housing_price.csv')
print(data.head())

#--------------把数据展示出来
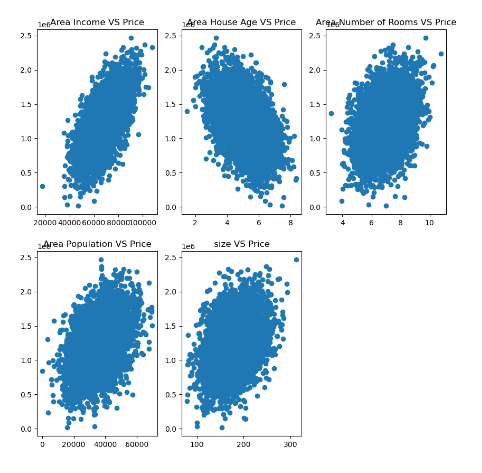
fig = plt.figure(figsize=(10,10))
fig1 = plt.subplot(231)
plt.scatter(data.loc[:,'Avg. Area Income'],data.loc[:,'Price'])
plt.title('Area Income VS Price')
#--------------------------------------------------
fig2 = plt.subplot(232)
plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price'])
plt.title('Area House Age VS Price')
#--------------------------------------------------
fig3 = plt.subplot(233)
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price'])
plt.title('Area Number of Rooms VS Price')
#--------------------------------------------------
fig4 = plt.subplot(234)
plt.scatter(data.loc[:,'Area Population'],data.loc[:,'Price'])
plt.title('Area Population VS Price')
#--------------------------------------------------
fig5 = plt.subplot(235)
plt.scatter(data.loc[:,'size'],data.loc[:,'Price'])
plt.title('size VS Price')
#plt.show()

#-------------------------------单因子模型的实现，使用面积预测房价
X = data.loc[:,'size']
y = data.loc[:,'Price']
X = np.array(X).reshape(-1,1)
LR_1 = LinearRegression()
LR_1.fit(X,y)
predict_1 = LR_1.predict(X)
print(predict_1)
#用mes 和 r2 评估模型
MES = mean_squared_error(y,predict_1)
R2 = r2_score(y,predict_1)
print(MES,R2)
#可视化
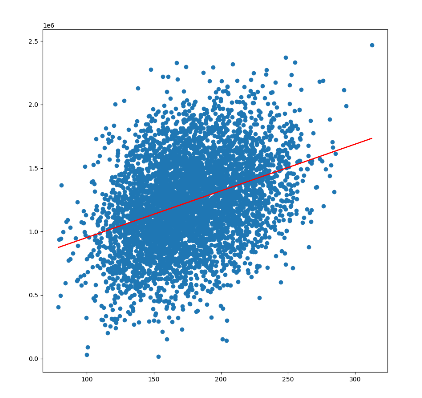
figer_result_1 = plt.figure(figsize=(10,10))
plt.scatter(X,y)
plt.plot(X,predict_1,'red')


#-------------------------多因子模型的实现
X = data.drop(['Price'],axis=1)
LR_Multi = LinearRegression()
LR_Multi.fit(X,y)
multi_predict = LR_Multi.predict(X)
MES = mean_squared_error(y,multi_predict)
R2  = r2_score(y,multi_predict)
print(MES,R2)

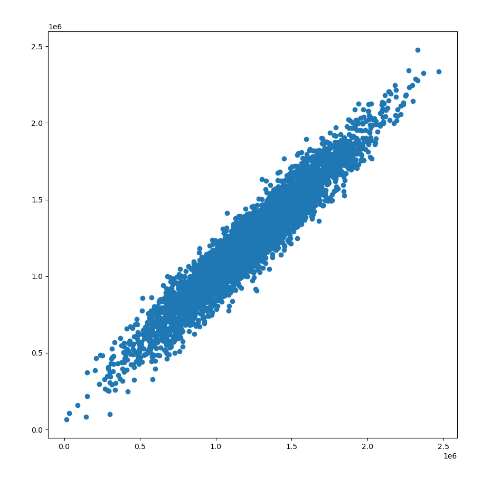
figer_result_multi = plt.figure(figsize=(10,10))
plt.scatter(y,multi_predict)
plt.show()

#预测
X_test = [65000,5,5,30000,200]
X_test = np.array(X_test).reshape(1,-1)
print(type(X_test))
predict_result = LR_Multi.predict(X_test)
print(predict_result)

#预测2
#X_test = pd.DataFrame([65000,5,5,30000,200])
#predict_result = LR_Multi.predict(X_test)
#print(predict_result)